Fenêtre de discrétisation

Plusieurs méthodes sont proposées afin de transformer une série continue de valeurs en une série discrète, c'est à dire en un nombre fini de classes.

Lors de la création d'une représentation choroplèthe, le nombre de classes ainsi que les valeurs limites de ces classes doivent être justifiées statistiquement et/ou thématiquement.

Les méthodes proposées par l'outil peuvent être utilisées telles quelles ou bien comme des guides de lecture et d'analyse préalables à la saisie manuelle des limites de classes souhaité.

Vue d'ensemble de la fenêtre de discrétisation

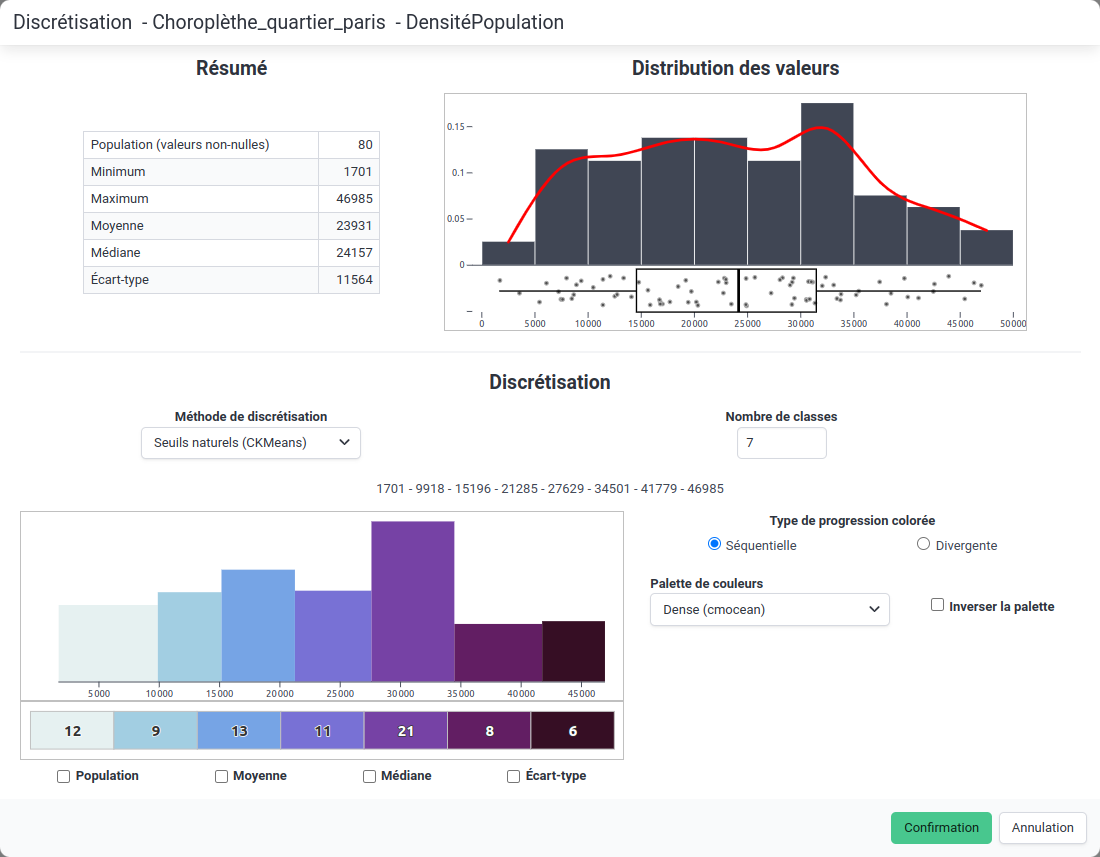Fenêtre de discrétisation

Plusieurs éléments sont présents dans cette fenêtre :

• Un résumé de la série de valeurs à discrétiser (nombre de valeurs non-nulles, moyenne, médiane, minimum, maximum, etc.),
• Un aperçu graphique de la distribution des valeurs (histogramme, courbe de densité et boîte à moustaches),
• Une section dédiée à la discrétisation (choix de la méthode, nombre de classes, choix de la palette de couleurs et visualisation du nombre d'entités par classe).

Méthodes de discrétisation

Quantiles

Cette méthode, parfois également décrite par le terme de "discrétisation en classes d'effectifs égaux" permet de former des classes qui possèdent toutes le même nombre d'individus.

Intervalles égaux

Cette méthode, parfois également appelée "amplitudes égales", permet de créer des classes qui possèdent toutes la même étendue.

Q6

Cette méthode (notamment démocratisée par l'outil PhilCarto), permet d'effectuer une discrétisation selon la méthode des quartiles tout en isolant les valeurs extrêmes : elle produit ainsi 6 classes. Les 6 classes sont définies avec les bornes suivantes : minimum, percentile 5 (0.05%), 1er quartile (25%), médiane (50%), 3ème quartile (75%), percentile 95 (95%), maximum.

Seuils naturels (algorithme CKMeans)

Cette méthode permet de créer des classes homogènes. En effet l'algorithme vise à trouver le nombre de classe souhaité en minimisant la variance intra-classe et en maximisant la variance inter-classe.

Seuils naturels (algorithme de Fisher-Jenks)

Cette méthode permet de créer des classes homogènes. En effet l'algorithme vise à trouver le nombre de classe souhaité en minimisant la variance intra-classe et en maximisant la variance inter-classe.

Dépréciation

Cette méthode est désormais dépréciée en faveur de la méthode CKMeans donnant de meilleurs résultats (les entités sont classées comme dans la méthode de Fisher-Jenks mais avec des limites de classes plus faciles à lire) en un temps de calcul bien plus court. Nous vous conseillons donc d'utiliser la méthode CKMeans à la place.

Moyenne et écart-type

Cette méthode propose de former des classes en fonction de la valeur de l'écart-type et de la moyenne. Ce mode de discrétisation ne permet pas de choisir directement un nombre de classes mais permet de choisir la portion d'écart-type qui correspond à la taille d'une classe ainsi que le rôle de la moyenne (utilisée comme borne de classe ou comme centre de classe).

Progression géométrique

Cette méthode de discrétisation permet de créer des classes dont les limites sont définies par une progression géométrique : chaque classe est définie par un multiple de la précédente.

Head / Tail Breaks

Cette méthode de discrétisation permet de créer des classes pour des séries très déséquilibrées à gauche (avec beaucoup de valeurs faibles et quelques très fortes valeurs).

Moyennes emboitées

La méthode des moyennes emboitées permet de créer des classes de manière hiérarchique. Chaque classe est définie par la moyenne des valeurs de la classe parente (ou de l'ensemble de la série pour les deux premières classes).

Le nombre de classes qu'il est possible de choisir pour cette méthode est donc nécessairement une puissance de 2 (2, 4, 8, etc.).

Saisie manuelle

Il est également possible de saisir manuellement les bornes de classes.

Cette méthode peut être très utile notamment pour :

• pour créer de "jolies" limites de classes, ou au moins les ajuster, après avoir effectué une discrétisation automatique avec les quantiles ou les seuils naturels par exemple,
• pour réutiliser des limites de classes déjà définies dans un autre contexte afin de comparer des cartes.

Noter qu'il est possible de coller depuis le presse-papier des limites de classes séparées par des tirets (par exemple : 0 - 10 - 20 - 30 - 40) comme montré dans l'animation ci-dessous.

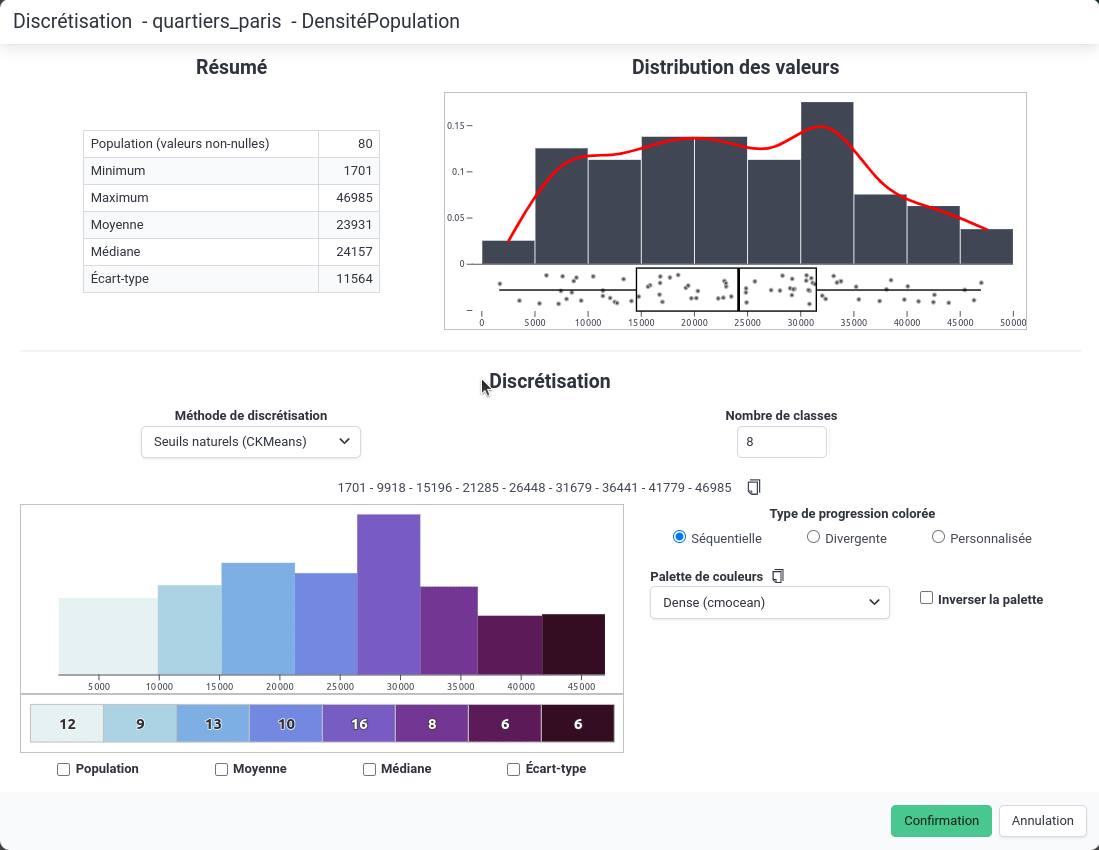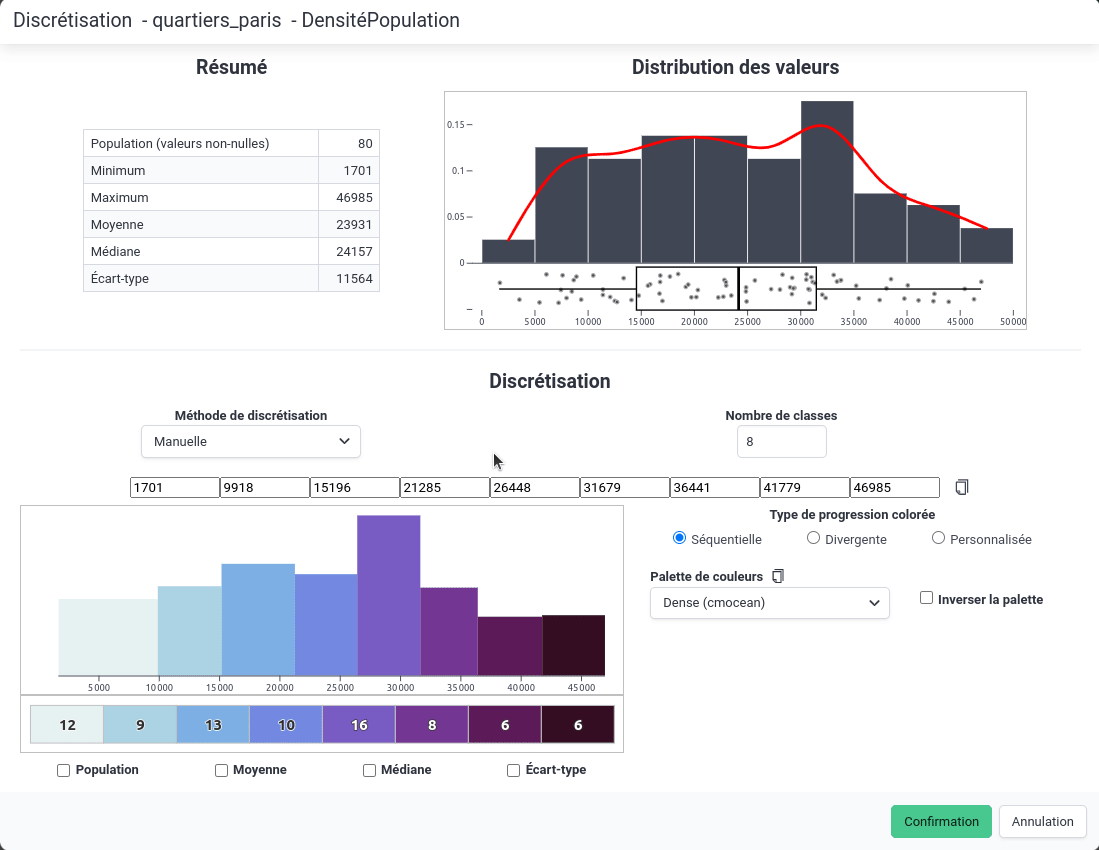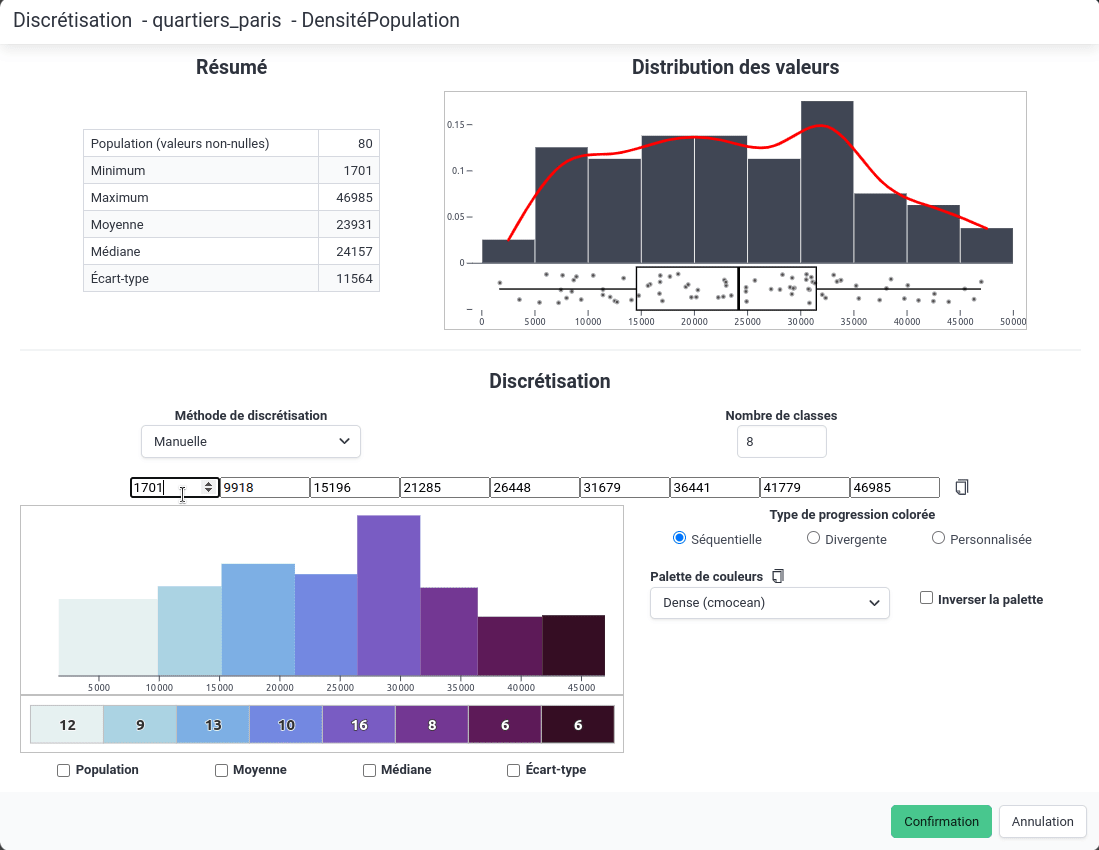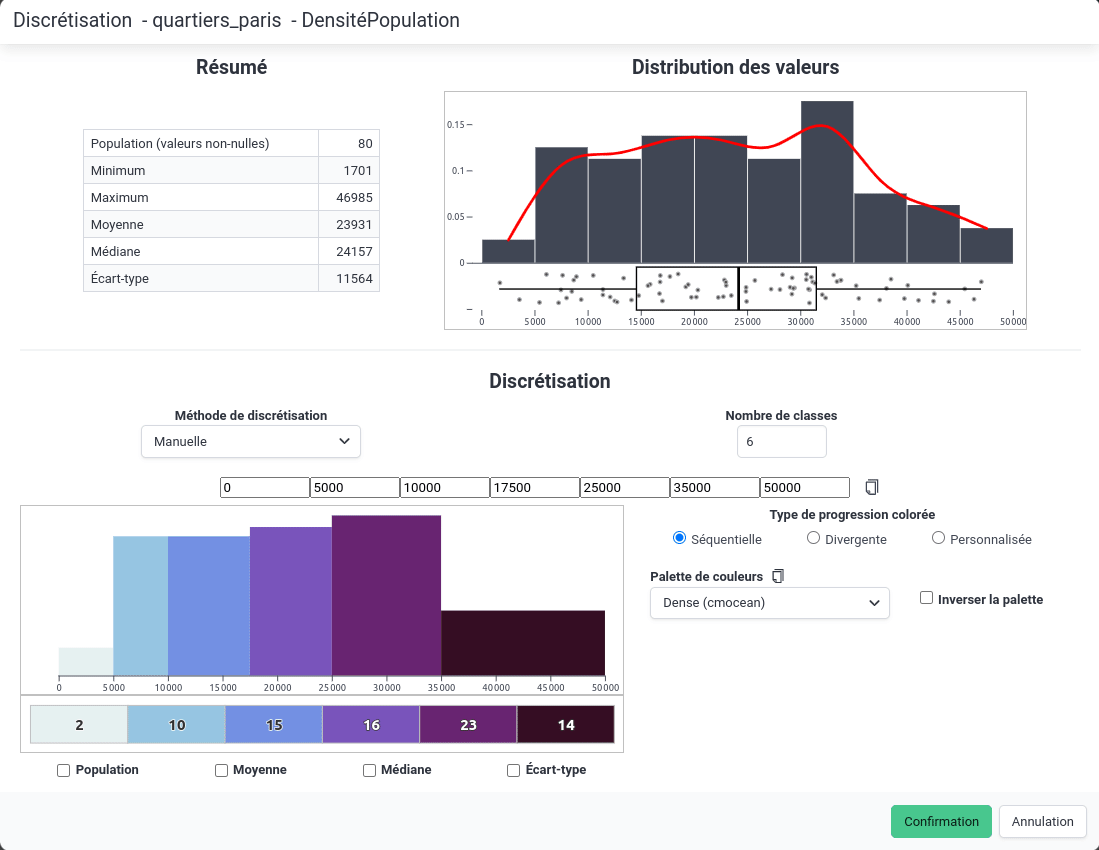Saisie manuelle des limites de classes

Choix d'une progression de couleurs

Deux types de progressions colorées sont disponibles dans Magrit :

• Les palettes séquentielles : elles sont utilisées pour représenter des données ordonnées de manière continue.
• Les palettes divergentes : elles sont utilisées pour représenter des données ordonnées autour d'une valeur centrale (par exemple, une moyenne, ou la valeur zéro, etc.).

Les palettes de couleurs proposées sont issus de la bibliothèque dicopal qui propose des palettes en provenance de nombreux fournisseurs : ColorBrewer, Fabio Crameri's Scientific Colour Maps, CartoColors, CmOcean, Matplotlib, Light & Bartlein, MyCarta, Tableau, Joshua Stevens, etc.

Ces palettes peuvent être générées pour le nombre de classes désiré. Pour les palettes divergentes, des options permettent de choisir si une classe centrale (neutre) doit être présente ou non et la position de cette classe (ou du point d'inflexion le cas échéant), permettant de générer des palettes divergentes asymétriques.

Il est également possible de choisir une palette de couleurs personnalisée en cliquant sur l'option "Palette personnalisée" (voir ci-dessous).

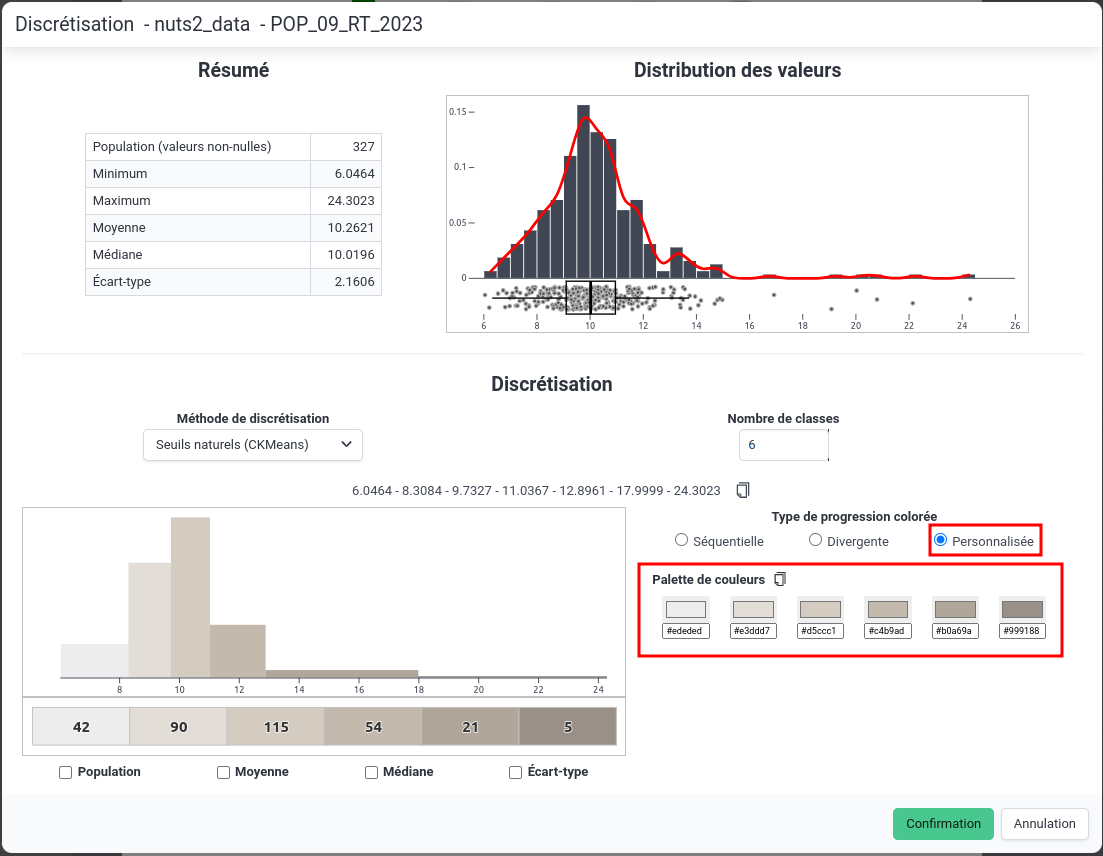Fenêtre de discrétisation avec palette personnalisée

En savoir plus sur le choix d'une discrétisation en cartographie thématique

Vous pouvez consulter l'article Géovisualisation des discrétisations : une petite application pédagogique (par Laurent Jégou), dans la revue MappeMonde n°119, qui met en avant, de manière interactive, l'importance du choix d'une discrétisation adaptée en cartographie.